データ構造とアルゴリズム Advent Calendar 2019の1日目の記事です。
2日目は@yurahunaさんによる「三角形分割の数え上げとランダムサンプリング」です。
6月にグレッグ・イーガン氏のHPで見つけた順列生成アルゴリズムについてブログを書きました。
そのあとに元ネタの論文1を読んでいたのですが、おもしろい順列生成アルゴリズムを含んでいたのでGoでライブラリ化してみました。
deltam/perm: Permutation generator based on group theory written in Go
自分のベンチマークでは再帰関数で実装したナイーブなアルゴリズムより33%ほど早いですが、高速さが売りというよりも「順列への最小限の操作セットのみを駆使して順列生成できないか?」という研究の流れから出てきた副産物的なアルゴリズムです。
ただその最小限の操作セットを駆使するアイデアが面白く、最終的に出来るルールが非常にシンプルで実装も短くできるのでアドベントカレンダーに乗じて紹介しようと思います。
まずアルゴリズムの背景となる論文の内容を紹介し、その結果をルール化して順列生成のプログラムを作ります。
順列の群とグラフとその経路
元ネタはこのAaron Williams氏の論文です。
Hamiltonicity of the Cayley Digraph on the Symmetric Group Generated by σ = (1 2 … n) and τ = (1 2)
(同著者の若干読みやすい別の文書2もあります。グレッグ・イーガン氏が最小超置換に関連して解説している記事3もあります)
この論文は順列の集合に次の2つの関数を定義して群としたものを対象としています。論文ではギリシャ文字で書いてますがこの記事ではsigma,tauと表記します(入力が面倒だった…)。
sigma: (1,2,...,n) -> (2,3,...,n,1) // ローテーション
tau: (1,2,...,n) -> (2,1,...,n) // 先頭2つのスワップ
sigmaは順列をひとつずつローテーションしていくのでn回やると元に戻ります。tauは2回でもとに戻ります。
ふたつを組み合わせると任意の連続した2つの記号をスワップすることができるので、ある順列が与えられればすべての順列をsigma, tauで作り出すことが出来ます。順列の集合とsigma/tauを合わせたものは対称群(Symmetric Group)になります。
さらにこの対称群の順列を頂点、sigma/tauで移り変わる関係を辺として有向グラフにします。このように群から作ったグラフをケーリーグラフ(Cayley graph)というそうです。
n=4の順列でケーリーグラフを作って図にしてみました。実線がsigmaで点線がtauです。

図1 順列n=4のケーリーグラフ
このグラフ上に 「すべての頂点を一度だけめぐる経路は存在するのか?」 というのがこの論文の解決したい問題(通称 Sigma-Tau Path Problem 2)です。グラフの言葉でいうとハミルトン路(Hamilton path)は存在するのか?ということです。
ハミルトン路が存在するなら「ある順列から始めてsigma/tauのどちらかの操作を繰り返すことにより毎回違う順列にするような操作の順序が存在する」ということがわかります。
この論文は 「すべての n についてハミルトン路は存在する」 ということを証明しました。それを生成するためのシンプルなルールも提示しています。
これはたとえばトランプの山札に対して「一番上の1枚を一番下に移動する」と「上から1枚目と2枚目を入れ替える」のどちらかを $52!$ 回繰り返して毎回違う順番にすることができるということで、なんだか不思議な結果に思えますね。
余談ですが、論文ではさらに「 n が奇数ならハミルトン閉路(Hamilton cycle, 始点と終点がつながる)が存在する」ということも証明しています(偶数なら存在しないことは Rankin’s Campanological Theorem からわかっているそうです4)。
「 $n \geq 3$ の奇数のケーリーグラフにはいつでもハミルトン閉路が存在するか」という問題はクヌース先生のThe Art of Computer Programmingでも最高難度(48/50)の問題として挙げられているもので(4巻 7.2.1.2 問題74)、この論文はそれを解決しました(でも順列生成にはハミルトン路だけで十分なのでハミルトン閉路生成について詳しくは解説しません!)。
輪っかとジグザグ
論文では上記のようなケーリーグラフには「ちょうど2つの共通部分を持たないなサイクルカバーが存在する」ということを証明し、2つのサイクルをつなぎ合わせることでハミルトン路を構成して証明しました。
サイクルカバー(cycle cover)はグラフ上のループで同じ頂点を2回以上通らないものです。(正式には vertex-disjoint cycle cover , 日本語だと閉道というらしいですが慣れていないのでサイクルカバーと表記します)
全部の辺を表示すると煩雑なのでsigma辺だけ表示するとこのようなグラフになります。
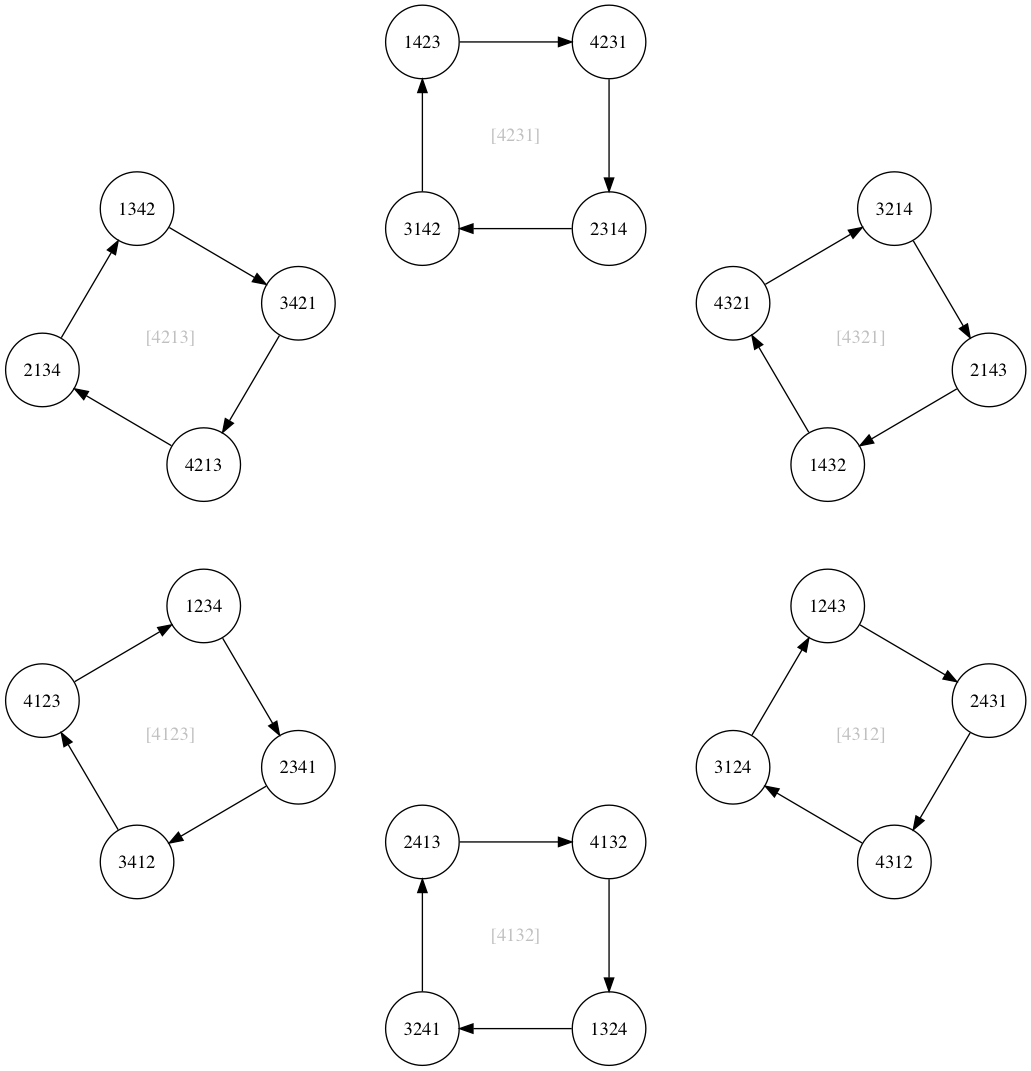
図2 順列n=4のsigmaサイクル
この図2と最初の図1を見ると次のことがわかります。
- sigma辺はローテーションなので n 回でもとに戻るサイクルカバーを作る(sigmaサイクルと呼ぶことにする)
- tau辺は異なるsigmaサイクルにつながっている
- すべての頂点はsigma,tau辺が2つずつあり、それぞれ出発する方向と到着する方向がひとつずつである
どうにかsigmaサイクル同士をtau辺で繋いで大きなサイクルにする手順が考えられないか。
そこでこのようなルートを考えます。まず適当な頂点から始めてtau辺を通り、つぎにsigma辺を逆にたどるのを繰り返します(「有向グラフなのに逆に進んでOKなの?」と思うかもしれませんが、最終的に逆方向の辺は消去されます)。
4321から始めるとこのように移動します。
4321 tau-> 3421
sigma<- 1342
tau-> 3142
sigma<- 2314
tau-> 3214
sigma<- 4321 (最初に戻る)
図2の上半分のレイアウトに合わせて描くとこんなかんじ。

図3 4321を始点とする交互サイクル
このルートがサイクルをつなげる鍵で、論文では 交互サイクル(alternating-cycle) と呼ばれています。これを接しているsigmaサイクルと合成してみます。
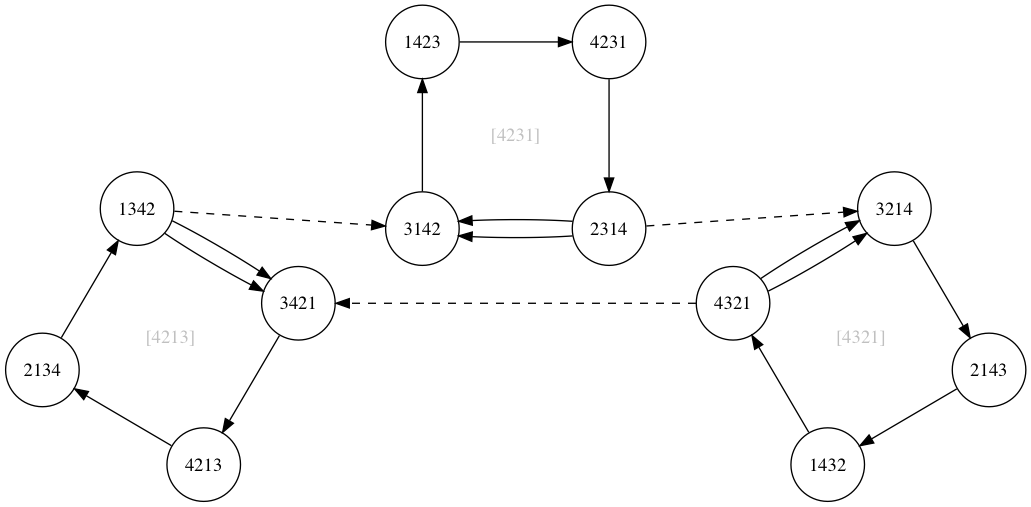
図4 交互サイクルとsigmaサイクルの和
二重になっている辺を削除するとこうなります。

図5 交互サイクルとsigmaサイクルの対称差
3つのsigmaサイクルがつながって大きなサイクルになりました。
このようにsigmaサイクルと交互サイクルの対称差(symmetric difference)を取ったものもまたサイクルカバーになります。 なぜでしょう?
サイクルカバーの頂点の持つ辺の向きを考えてみます。頂点をちょうど一度だけ通るのだから到着する方向と出発する方向の二本を持っているはずです。
交互サイクルの辺の向きも見てみましょう。図3のレイアウトを変えたものが以下です。
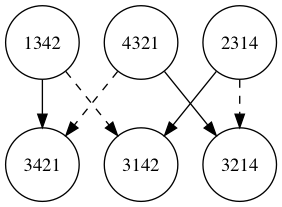
交互サイクルはそれぞれ二本の辺を持ちますが、両方とも到着する方向 or 出発する方向のどちらかです。そして二本のどちらか一方だけsigma辺です。
sigmaサイクルと対称差を取った場合、sigmaサイクルのある頂点は到着する or 出発する方向のsigma辺を失いますが、同時に同じ方向のtau辺を得ます。つまりそれぞれの頂点は持っている辺の個数と方向だけ見ると変わっていません。
頂点の持つ辺の方向というサイクルカバーの特性が変わらずtau辺によって異なるsigmaサイクル同士がつながるので、大きなサイクルカバーを作ることができるという仕組みです。
論文によると対称差をつかう手法は17世紀から知られていたそうですが、交互サイクルという形にして絶妙に使いこなしたことがこの論文の最大のハックだと思います。
交互サイクルの始点
sigmaサイクルと交互サイクルで大きなサイクルカバーができるのはわかりましたが、上記の例は3つのsigmaサイクルを繋げただけです。できるだけ多くつなげるにはどうしたらいいでしょう? 辺や頂点がかぶらない作り方をしたいですね。
まずは交互サイクルの特性をもうすこし調べてみましょう。以下は4321から始まる交互サイクルの頂点を並べたものです。
4 3 2 1
3 4 2 1
1 3 4 2
3 1 4 2
2 3 1 4
3 2 1 4
4321から3の位置は最初と二番目を行ったり来たりしています。3を取り去るとそれ以外の並びは421とローテーションで一致します。始点の二番目の文字とそれ以外の循環的な並びが違うなら交互サイクルも頂点や辺が共有されることはありません。
$nmr…$ という順列の並びを考えます。nを先頭に固定して $nmr$ で始まる順列の集合を表したものです。これを交互サイクルの始点にすると最初と二番目を交互に移動する数字が m になり、循環的な並びは $nr…$ になります。
じつはこの $(r,m)$ の組みを次のように選ぶとsigmaサイクルを全部つなげることができます5。
$$
(1,2), (2,3), … , (n-2, n-1), (n-1,1)
$$
$$
\begin{equation}
\therefore m = (r \bmod{n-1}) +1 \tag{1}
\end{equation}
$$
$n=4$ の場合は次の3つの始点から交互サイクルを作ればOKです。
(1,2) => 4213
(2,3) => 4321
(3,1) => 4132

図6 4213,4321,4132から始まる交互サイクル
sigmaサイクルと対称差を取ると灰色の辺が消えて大きな2つのサイクルになっています!

図7 交互サイクルとsigmaサイクルから作った2つのサイクルカバー
2-Cycle Rule
上記の交互サイクルの選び方をするとかならず長さ $2(n-1)$ の Small Cycle とそれ以外全部の Large Cycle になるそうです。なぜそうなるのかと説明したいところなのですが、論文では組合せ論のRotation systemというものを使って証明していて、私にはよく分かりませんでした…6
掴んだニュアンスだけでふんわりと説明すると交互サイクル同士はsigmaサイクルを経由してつながる木構造のような形になるのですが、式(1)の選び方だと根の部分にhubと呼ばれるサイクルができてしまいそれが Small Cycle になるようです。
さて図7のところまで来ました。式(1)の関係で交互サイクルを作っていて交互サイクルのsigma辺は消えていることを考えると、図7を作るためのルールが考えられます。ルールはある頂点からsigma辺、tau辺のどちらの進むかを決めることができればサイクルカバーを作れるのでOKです。
ある順列の二番目の数字を $m$ とし、循環的に $n$ の右隣にある数字を $r$ とします( $n$ が最後尾にある場合はrは最初の数字)。ただし $r=m$ だったら $m$ を抜かして三番目の数字を $r$ とします。そう決めると図7の2つのサイクルを作るルールを次のように書けます。
$$\begin{eqnarray}
cycle(p) = \begin{cases}
tau(p) & \text{if} \quad m = (r \bmod{n-1})+1 \\
sigma(p) & \text{else}
\end{cases} \tag{2}
\end{eqnarray}$$
小さい輪と大きい輪をつなげるポイント
ふたつのサイクルカバーを作るルールが得られましたが、それだけでは全体の順列生成に使えません。どこかで切って繋げてひとつながりの経路にしたいですね。
さて上記の(2)のルールを逆順に並べた順列に対して適用してみましょう(n=4なら 4321 )。実は逆順の順列は必ず Small Cycle に属します。
4321: m=3, r=2 -> tau -> 3421
3421: m=n -> sigma -> 4213
4213: m=2, r=1 -> tau -> 2413
2413: m=n -> sigma -> 4132
4132: m=1, r=3 -> tau -> 1432
1432: m=n -> sigma -> 4321 (最初に戻る)
見ての通り、逆順4321から始まる Small Cycle は n の位置が最初か2番めでそれ以外はn-1の逆順のローテーションになり、長さが $2(n-1)$ になります。 $n!$ 個の頂点の中の $2(n-1)$ 個のサイクルなのでSmall Cycleと名付けられているわけです。
Small Cycle では 4321 からtau辺をたどるのですが、そこでsigma辺に進むと 4 の位置関係が崩れるので Large Cycle に移動します。論文でもここを切り分けて繋げるポイントにしていますが、実装上でも逆順判定をする処理をSmall Cycle、Large Cycle両方の終了を判定に使えるので都合がいいです。
4321 から 3214 へのsigma辺を足してひとつながりにしたものが以下です。4321 で切り分けるため経路の始点を $tau(4321)=3421$ にしています。

図8 n=4のハミルトン路(Hamilton Path)
順列生成ルール
切り分けポイントを含めた最終的なルールをまとめます。
$$
\begin{eqnarray}
path(p) =
\begin{cases}
tau(p) & \text{if} \quad m = (r \bmod{n-1})+1 \land p \ne n,n-1,…,2,1 \\
sigma(p) & \text{else}
\end{cases} \tag{3}
\end{eqnarray}
$$
論文では Definition 3. と書いているものと同等のものです(論文では記述の簡潔さのためか逆順ルートで生成するルールになっている)。
実装
ルール(3)をGoで実装してみたのが以下です7。ブラウザで動作確認したい場合はGo Playgroundをどうぞ。
package main
import "fmt"
const N = 4
func main() {
p := make([]int, N)
all := 1
for i := 0; i < N; i++ {
p[i] = N - i
all *= i + 1
}
tau(p)
fmt.Println(p)
for i := 1; i < all; i++ {
if ruleCycle(p) && !isSmallCycleEnd(p) {
tau(p)
} else {
sigma(p)
}
fmt.Println(p)
}
}
func sigma(p []int) {
f := p[0]
copy(p[0:N-1], p[1:N])
p[N-1] = f
}
func tau(p []int) {
p[0], p[1] = p[1], p[0]
}
func ruleCycle(p []int) bool {
r, i := 0, 0
for p[i] != N {
i++
}
if i == 0 {
r = p[2]
} else {
r = p[(i+1)%N]
}
return p[1] == r%(N-1)+1
}
func isSmallCycleEnd(p []int) bool {
for i := 0; i < N; i++ {
if p[i] != N-i {
return false
}
}
return true
}
出力される順列にかぶりがないか確認します。
$ go run main.go
[3 4 2 1]
[4 2 1 3]
[2 4 1 3]
[4 1 3 2]
[1 4 3 2]
[4 3 2 1]
[3 2 1 4]
[2 1 4 3]
[1 2 4 3]
[2 4 3 1]
[4 3 1 2]
[3 1 2 4]
[1 3 2 4]
[3 2 4 1]
[2 3 4 1]
[3 4 1 2]
[4 1 2 3]
[1 2 3 4]
[2 1 3 4]
[1 3 4 2]
[3 1 4 2]
[1 4 2 3]
[4 2 3 1]
[2 3 1 4]
$ go run main.go|sort
[1 2 3 4]
[1 2 4 3]
[1 3 2 4]
[1 3 4 2]
[1 4 2 3]
[1 4 3 2]
[2 1 3 4]
[2 1 4 3]
[2 3 1 4]
[2 3 4 1]
[2 4 1 3]
[2 4 3 1]
[3 1 2 4]
[3 1 4 2]
[3 2 1 4]
[3 2 4 1]
[3 4 1 2]
[3 4 2 1]
[4 1 2 3]
[4 1 3 2]
[4 2 1 3]
[4 2 3 1]
[4 3 1 2]
[4 3 2 1]
$ go run main.go |sort|uniq|wc -l
24
順列生成できました!
2018年の論文2にはC言語による実装も載っているので気になる方はチェックしてみてください。
ライブラリでの実装
もともと最小超置換探索のアルゴリズムを理解するためにClojureコードを書いてました。そこでグレッグ・イーガン氏の記事3に上記アルゴリズムをアレンジしたものが The Williams Construction として紹介されていたので興味本位で実装してみました(superperm.williams)。
deltam/clj-superpermutation: Clojure library for finding minimal superpermutation
Clojureには集合リテラルがあるので数学的な処理を書くのに便利です。REPLも試行錯誤して理解を深めるのに助かりました。実はこの記事の図もこのClojurerコードとGraphvizで作っています。
おもしろいアルゴリズムだったのでGoのライブラリに切り出してみました。Goの実装はベンチマーク、プロファイリングなど取って出来る限り高速化してます。
deltam/perm: Permutation generator based on group theory written in Go
上記の実装コードでは1…nの順列でしたが、配列のインデックスにそのまま使えるようにライブラリでは0…n-1の順列にしています。配列を与えて順列のイテレータっぽく使えるようにも作ってあります(詳しくは Usage を読んでください)。
ライブラリでは上記コードのように $n!$ 個を出力してストップするのではなく順列の並びから終了判定しています。これによりたとえ $1000!$ 個の順列でも桁あふれすることなく生成し続けることができます。現在の順列を保存しておけばそこからすぐに生成を再開できるのも良いところですね。
ローテーション操作を多用するので例えば「先頭が 1,2,.. の順列だけスキップする」のようなことは出来ません。生成順序に癖があるので実用的かどうかは分かりません(そもそも順列生成ってどこで実用されるのか?)
より良い実装としてはsigma/tauが高速になるようなデータ構造を選ぶというのが考えられます。そこでローテーションが多用されるならリストをつかったほうが早いのではと思いcontainer/listで書き換えてみたのですが、逆に遅くなってしまいました。ビルトイン関数の copy が思ったより早かったようです。あとはビット列で表現するとsigmaがビットシフトで出来るので早くなりそうと思いましたが、そこまでは高速化に情熱が持てなかったのでこちらは試してません。
なにか面白いアイデアありましたら issue / PullReq をください!
余談
TAOCPでの言及
紹介した論文が発表される前に書かれた The Art of Computer Programming, Volume 4, p.333, 少数の生成器の使用 ではsigma-tauのやり方を次のように紹介しています。
Ruskey, Jiang, Weston [Discrete Applied Math. 57(1995), 75-83] は, n=5のσーτを全数探索することによって5つの本質的に異なるHamiltonグラフが存在することと, そのうちの1つ「最も美しい」図22(a)に示すものを発見した。(中略)残念なことに, 彼らが発見した解には, はっきりとした論理的な構造を持たない。演習70にいくらか複雑さが少ない経路を述べるけれども, その経路でさえ単純であるとは言い難い。したがって, σ-τをのやり方は, もっと n が大きな値の場合には, 新しい構成方法が見つからない限り, あまり本気で使う気にはならない。
今回紹介した順列生成アルゴリズムは「論理的な構造」を持つ「新しい構成方法」ではないでしょうか。 おそらく改訂版に載るのでは?
順列リボンの比較
TAOCPでは順列生成で数字が移動する様子を折れ線グラフでリボンのように可視化する見せ方をしています。同じようにこのアルゴリズムでの移動を可視化してみました8。比較用に順列を辞書式順序に並べたリボンもつくってみました。


図8 n=4のハミルトン路(上)、辞書式順序の順列(下)
sigmaサイクルをたどっているところは斜めのラインが続いていてストライプ模様になっていてきれいな気がします。クリスマスの飾り付けっぽいリボンになりましたね(無理やりなアドベントカレンダー要素)
まとめ
順列とsigma/tau操作による群をグラフ化してそこにハミルトン路が存在するということを証明した論文を紹介しました。ハミルトン路の生成ルールは簡潔に書くことが可能で、実装もおこないました。
Goのライブラリにしたので使ってみてください!
おわり。
Hamiltonicity of the Cayley Digraph on the Symmetric Group Generated by σ = (1 2 … n) and τ = (1 2) ↩︎
Superpermutations — Greg Egan, The Williams Construction ↩︎ ↩︎
The Art of Computer Programming Volume 4A Combinatorial Algorithms ↩︎ ↩︎
$n \ge 3$ の奇数の場合、 $(1,2), (2,3), …, (n-2,n-1), (n-1,2)$ と $1,n,2,3,…,n-2,n-1$ を交互サイクルの始点に選ぶとハミルトン閉路になるそうです。 ↩︎
同著者の2018年の論文2の最後の一文にRotation systemを使って証明に対して
"Our future work is to simplify the proof in [10] using the approach taken in this paper."とあるので今後に期待したい。 ↩︎ハミルトン閉路バージョンのルールのGo実装もつくりました Go Playground ↩︎
n=5のハミルトン閉路のリボンもつくってみた
↩︎
0 件のコメント:
コメントを投稿